Original Odhner LUSID
A recent find, and one of the most whimsical, counterintuitive and plain ridiculous pinwheel calculators ever to be manufactured. I have been dying to get my hands on one, and now that it is in the collection, I was happy to be able to document how the machine actually functions, since it had to be disassembled anyway due to a number of problems.
This, N° 68369, is the early version with the butterfly clearing screws. I though I was on to something when I got LuSiD N° 68382, which had clearing cranks intead of butterflies. However, on rechenmaschinen-illustrated, there is a N° 78129 with butterflies, and I have also seen N° 89831, which also has butterflies. Other Odhner models carry butterflies until at least in the 90000 range of serial numbers, so either they were not very consistent in the Odhner factory, or the carriage of LuSiD 68382 was replaced or repaired later. A repair is not as simple as taking off the butterfly and putting a crank in its place, so someone invested a bit of time and parts. This machine was not functional when it came to me, which turned out to be down to incorrect reassembly after an attempted repair of some sort. Not being able to see how it ought to function prior to taking it apart was not conducive to a relaxed and stress-free repair though. After shifting back the coupling wheel for the Mult/Div lever one tooth, suddenly everything freed up as it should with the crank in the rest position, and the rest was a question of some light cleaning and reassembly. Here is the complete and reassembled machine:




In the mean time, I have unearthed another example, N° 65694, which is even earlier than the one discussed above, N°68369. There are some interesting differences between the two. They are not far apart in serial number, which leads me to belive that this kind of machine is the very earliest type of Lusid made by Odhner. The main differences are in the base, the switch on the carriage for shifting from decimal to £sd operation, and the comma sliders.
Some pictures:




Serial N°:

End view of the carriage of the early (top) and later (bottom) machine


And finally, the two machines together for a direct comparison, the later machine is on top:

The following explanation of how the LuSiD operates is an extract from an article I wrote for Historische Bürowelt, which was published in issue 110, december 2017. It is reproduced verbatim, with permission.
The Odhner LuSiD
by Cris Vande Velde and Martin Reese
The Odhner LuSiD (£ s d, or pound, shilling, pence) was a specialty machine adapted for calculation in non-decimal currency or measures.

Figure 1 Early version of the Odhner LuSiD, serial n° 65394
Several versions are documented in Martin (first mention of this machine the literature in 1925), including a drawing of a “Lusid type G” of very limited capacity, which is suitable for calculations in both non-decimal currency and non-decimal weights. The model list in Martin is more a list of several types of problems, which use different functions in the various registers. All of these functions (except the handling of non-decimal weights) are incorporated in the final, and probably only, commercial form of the machine which can still be found today. The authors are unaware of any other type of LuSiD having survived, with one exception: the very early machines have no lever on the register that allows to switch the counter register from non-decimal to decimal.
Due to the very specific nature of the calculations needed, the usability of the machine is somewhat compromised, and it takes a very clear head and some exercise to manage to make sense of the results.
So first, two or three words about the non-decimal currency system in the UK that was used up to February 15th, 1971. The basic currency was the UK pound, £. A pound was divided into 20 shillings (s), which were each divided into 12 pence (d). Up to 1961, farthings (¼ penny) were also used, to yield e.g. 72£ 15s 5d ¾, or, in a different notation, £72.15.5 ¾. Obviously, such a currency system leads to big problems when multiplying and dividing, both mechanically and by hand – since the carries for pennies need to happen at 12, and the carries for shillings at 20, the only practical way of doing machine multiplications was to convert the whole amount to decimal fractions of pounds – e.g. 9s 11 ¼ d or £0.9.11.¼ would equal £0.497 – this decimal fraction could then be multiplied or divided on a regular calculating machine.
Enter Original Odhner Aktiebolaget in the early 1920s. From the patents, it is quite obvious that they had quite a good understanding of what was needed to make calculations with £ s d (nearly ...) effortless. The only problem is that the mechanical compromises that were needed, made the machine all but intuitive to use.
There are three important elements that distinguish the Odhner Lusid from a regular Odhner calculator –
The first element, patented in Sweden on April 22nd 1922, and in the UK as nr. 196,271, is a mechanical converter that automatically converts decimal fractions of pounds to shillings, pennies and fractions of pennies. In the final machine, it is located on the far right hand side of the carriage, and it always functions completely independently of the rest of the machine. All it does is to convert the final three digits in the regular result register, which for a particular fixed position of the carriage correspond to decimal fractions of pounds, to an amount in shillings, pence and farthings. This is done by an ingenious combination of two wide numeral rolls, and a shroud with holes (see figures 1, 2 and 3). It results in a total of 1000 possible combinations of numeral rolls and shroud, that list everything from d 0 over ¼ , ½, ¾ , ... all the way up to s 19.11¾. This corresponds approximately to d ¼ for every 0.001 increment in the result register – there are 240 pence in a pound, so that would mean 960 farthings or quarter pence. How are the 40 missing farthings accommodated? That is easy – it is done by rounding. Both for £0.037 and £0.038, the result is 9 pence, and both for £0.012 and £0.013 the result is 3 pence. Since this rounding occurs twice during the increment of one shilling to the next, and there are 20 shillings in a pound, we have found our 40 extra values we needed.
Mechanically, the way the conversion is done is also very interesting (see Figure 2). Since the conversion acts on decimal fractions of pounds, and decimal conversion of pounds to pennies to the nearest ¼, is approximately equivalent to £0.001, the converter operates on the three rightmost result wheels. It transfers the values in the result register to gears at the back of the carriage, sitting on three concentric shafts, then via intermediate gears again at the back of the carriage, on to another set of gears on the main axle of the carriage, but further to the right.
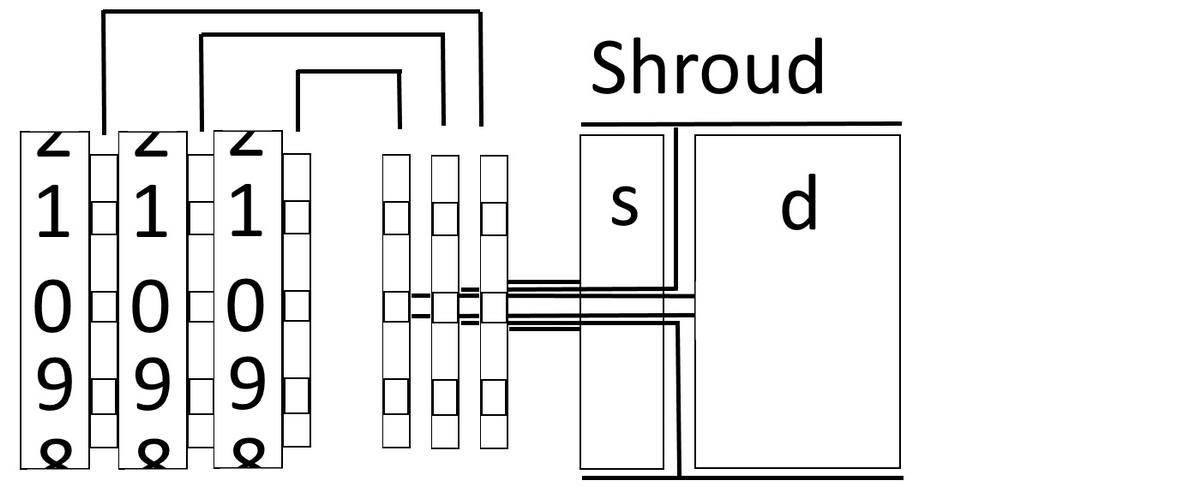
Figure 2 Schematic representation of the converter in the Odhner Lusid
These gears are then, again through concentric axles, directly connected to two numeral rolls, one for shillings (£0.1), and one for pennies (0.001£) (figure 3) - the middle gear (£0.01) operates the shroud with holes (figure 4).
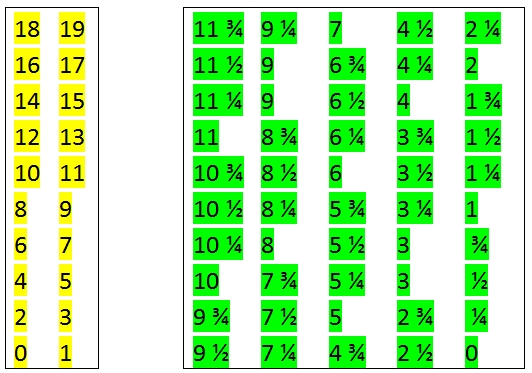
Figure 3 Shillings and pennies rolls in the Odhner Lusid unfolded

Figure 4 The shroud, pictured on the same scale as Figure 3
The shillings roll operates decimally, and has two columns of numbers of 10 numbers each, the even ones on the left (2,4,6...up to 18), the odd ones on the right (1,3...19). Adding £0.1 rotates the roll one position, incrementing the visible number of shillings by 2. The pennies roll, by contrast, has five columns of numbers, again with 10 positions each, incrementing by ¼, so that adding £0.001 visibly increments the roll by ¼ d (or a farthing). As mentioned higher, for rounding purposes, 3 and 9d occur twice in their respective columns. The shroud, operated by the £0.01 wheel, is very clever – it will increment the number shown by (on average, after rounding) 2.4d. It does so by rotating the shroud one position, and by virtue of its windows that are oriented along a double spiral, shifts the visible window in the shroud one place to the left. Since the column to the left displays the amount of shillings 2 ½ x higher (prior to rounding), the correct number now shows in the window. See figure 5 for examples.

Figure 5 Illustration of the operation of the converter. The green rectangles indicate what would be visible to the user with the carriage cover in place.
On reaching the leftmost column, the “carry” now happens by shifting the window for the shillings column from even to odd, e.g. from 10 (left) to 11 (right). If the shift has to happen again, from odd to even, an actual carry is also happening at this point in the £0.1 wheel in the decimal part of the register (e.g. 11 shifts to 10, which then rotates to 12 through the carry in the result register). Very clever indeed, and it ensures that any number that appears in the result register as the result of any of the 4 operations is automatically converted to non-decimal currency. To make this process more intuitive for the user and prevent possible confusion about which digits represent what, a switchable cover is provided which alternatively covers the three leftmost digits in the regular register (decimal fractions of pounds), or the s and d values shown in the converter, according to the needs of the user.
A video of the operation of the converter can be found here:
The second basic problem with non-decimal currency is the counting and carrying in the revolution register, when this is expected to be non-decimal. Here, the Odhner engineers again thought of a quite revolutionary system, which they also patented. The idea was that in order to count numbers in different bases (here 10, 12, 20 and 4) correctly, they ought to modify the counter finger in a dynamic and adaptable manner. That is to say, whereas in a normal decimal calculator one turn of the crank will always increment the counter register by 1 digit, things become a bit more complicated for non-decimal operation. The number added to the counter should then be dependent on the position one counts in. The first Odhner patent on these matters is submitted in Sweden on Sept. 19 1921, subsequently in Germany, nr. 414,402, and in the UK nr. 186,071in September 1922. (Figure 6) These patents accommodate this difficulty by providing a set of manual switches for the operator to modify the operation of the counter register, and thus choose whether he wishes to add 1 per revolution (for £), 2 (shilling position), or 2.4 / 24 (pence positions) to the counter register.
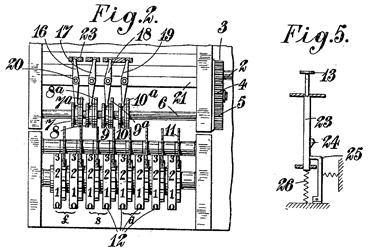
Figure 6 Odhner’s system for implementation of a nondecimal counter register (UK pat. 186,071) - this specific implementation was probably never commercialised.
This is the mechanical implementation of the well-known formula to convert £sd to decimal fractions of pounds: (£ + s/20 + d/240), or £1 = 20s = 240d The actual LuSiD machines that were built have automated this process, depending on the position of the carriage. This later modification is also patented in the same German patent, as well as in UK patent 211,420, as an addition to nr. 186,071. (Figure 7) The proposed form of the mechanism would be modified again in the actual machines (and moved from the right side of the carriage to the left side), for reasons that will become clear later. The mechanism works with a feeler finger that runs in a signal groove in the carriage, and in this way senses which number of counter teeth to use for a particular position of the carriage.
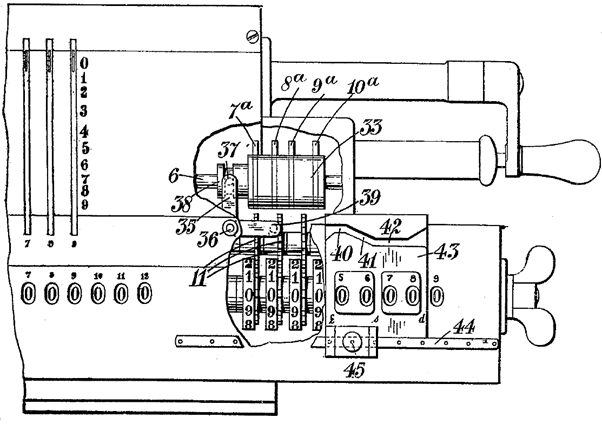
Figure 7 Odhner’s automatic, carriage-driven system for non-decimal counter register (UK pat. 211,420) – later switched to the left side of the machine.
The machine always assumes that one enters decimal fractions of pounds in the input, as the input register cannot accommodate shillings, pence or farthings. The machine will then, on multiplication or division to get a result in non-decimal currency in the counter register, automatically convert the decimal fractions of pounds into the correct units, i.e.
All of these changes are directed merely by the position of the carriage, which brings various sets of counting teeth into the correct position at the right time – the photographs below (Figure 8 and 9) will make this clear.

Figure 8 Automatically shifting set of counter wheels . Path of the pin is indicated in green – lever that shifts the counting teeth in yellow, changing gap between the gears in red.

Figure 9 Counter teeth in the process of counting. Counter register gears in the carriage marked in red, active counting teeth indicated in yellow. Number of active teeth indicated in green.
There is also a video to see the mechanism in action, which can be found here:
Carry in the revolution register is mostly taken care of – the decimal fractions of pennies carry at 10, the full pennies have a numeral wheel that counts up to 11 and carries at 12 into the shillings section, the shillings have a normal decimal carry, but there is no carry towards the pounds section at 20s, and the machine will show e.g. 24s – if this happens, then multiples of 20 need to be subtracted, and added to the pounds section – and this is not automatic. The pounds section then has normal carry at 10. To keep track of all of this, the two shillings numeral wheels and the one pennies numeral wheel that goes up to 12 are colored red, whereas the decimal fractions of pennies on the right are white, as are the full pounds on the left. When shifting the carriage, the leftmost red numeral wheel (10s of shillings) is skipped, and never actuated directly by the counter teeth, because it is only needed for carrying values from the lower shillings wheel.
It will not have escaped the technically curious that this system is all good and well, but it essentially fixes the decimal position in the machine – where the machine will switch from pounds to shillings is determined when the machine is built, thus limiting the input to a fixed decimal position. Since there are only 10 positions available in the input, and it may be desirable to input very minute decimal fractions of pounds in one case (e.g. for very cheap items – if a single nail costs £0.000438, how much would 1760 nails cost?), whereas another calculation may need over £10,000 in the input. Not to fear – the Odhner engineers have thought of this. The comma is not exactly floating, but they still managed to provide not one, but two sets of counting teeth, the one set three positions more to the left than the other (hence the extension on the left of the main body of the machine- this is where the second set of counting teeth lives). See Figure 10.

Figure 10 The two levers (green) for both sets of counting teeth, and the selection lever (red) to operate one or the other by engaging the central gear (yellow) into a set of dogs (cyan) on one of either concentric shafts, and blocking (magenta) the other. The green inset frame shows the other configuration of the lever.
There is a switch on the machine to change from “circle” decimal point to “triangle” decimal point. These symbols return in the input field of the machine, where the triangle sits between the 5th and 6th position from the right, and indicates the first (fixed) decimal point for non-decimal operation. The circle, the alternative decimal separator, sits between 8th and 9th position from the right. There are also two sets of double arrows marked on the carriage, accompanied by a circle for the left set, and a triangle for the right set, where the large arrow indicates the pounds position, and the smaller arrow the pence position. This is necessary because, as mentioned higher, the tens of shillings position is skipped when moving the carriage.
Now for the third modification from standard - if this were all, it would already be difficult to get one’s head around the machine, but the Odhner engineers went even further than this, and constructed the machine in such a way that the alien position-dependent counting of pennies and shillings in the counter register can be completely turned off, and replaced by normal tens’ carry in the entire counter register – a switch on the carriage, when pulled to the left, retracts the grooves used for sensing the carriage position (or replaces them with a straight groove in later machines), hence disabling the entire mechanism and always counting 1 in every position of the revolution counter. (Figure 11)

Figure 11 Switchable non-decimal tens’ carry. With the knob to the left, the levers remain where they are for the entire path of the carriage, and are unrestrained. Later LuSiD machines would have a grooved block over the entire width of the counter register, to fix the levers in place and prevent mishaps due to shaking or tilting the machine, which can cause the levers to move.
In this mode, the machine operates with a decimal counter register like any other normal pinwheel calculator, and the comma can be treated as floating. However, in this mode one needs to keep in mind that the one numeral wheel in the pence section of the carriage (which is in the 9th position from the left) will keep counting pennies up to 11 before carrying, because there is no conceivable mechanical way of changing that... This effectively limits the number of care-free digits in the counter register to 8. When the operator is however careful not to use abbreviated multiplication in the pennies position, he can enjoy more useable digits in the counter.
Now, all this being written – what can the machine do, and what sort of problems can you work out with it? There is an Odhner brochure that gives a flavour of possible problems:
The main points for working successfully with the Lusid are the following:
I will now show some pictures of successive problems 2 and 8 – say we want to figure out the price for 756 articles @ £1.16.9 ¾ each, and then discount the total with 12.5%. Since the decimal number in this problem is 756, and this has 3 digits, we set it up in the input with the triangle as the decimal point, for if we would use the circle, we only have 2 positions available, and we do need 3 in this case. Then we set the selection lever on the machine to “triangle”, clear the result and counter, check whether the selection lever on the carriage is set up for non-decimal currency in the counter register, and shift the carriage with the “triangle” pound arrow to the first pounds position. Now we crank £1.16.9 ¾ (=£1.16.9.7500) into the counter register. Because the counter has full carry (not exactly tens’ carry, but carry nonetheless ...), we can use the simple abbreviated algorithm where we crank until the number overshoots, then we tab one position to the right and crank in the other direction until we undershoot, tab to the right again and change direction to addition again, etc ... Once we cranked £1.16.9.75 into the counter, the result now reads £1391.10.3. If we now want to discount by 12.5%, we shift the cover on the carriage to see the decimal equivalent of £1391.10.3, which is 1391.513. This we set up in the setting register, still with the triangle decimal point, we clear the counter register, switch the counter register to decimal with the knob on the carriage, set the machine to “div” and crank in 0.125 to subtract 12.5% from the previous result.



Figure 12 Example calculation (see text). Top: result in £sd, middle: conversion to decimal, bottom: machine in decimal mode, subtracted (0.125 x 1391.513) to get £1217.11.5 ½
A video of this calculation can be found here:
