Coordinate transformations with double machines and the B183
Double and triple calculators were used a lot in the land registers in Germany, because historically they used a number of different coordinate systems that originated from the different German states before the unification in 1870, and from subsequent changes in legislation on which coordinate system to use and which not. The end result was that well into the 1960s the land registers were a complete mess. The calculations to transform the coordinates from one system into another were long and tedious. This article intends to show with a very practical example why double calculators were so popular at land offices in Germany, and why the Brunsviga 183 was even an improvement on that.
It is the rotation of the grid, which necessitates exchange between x and y, that makes coordinate transformations so tedious.
We will calculate a simple example -
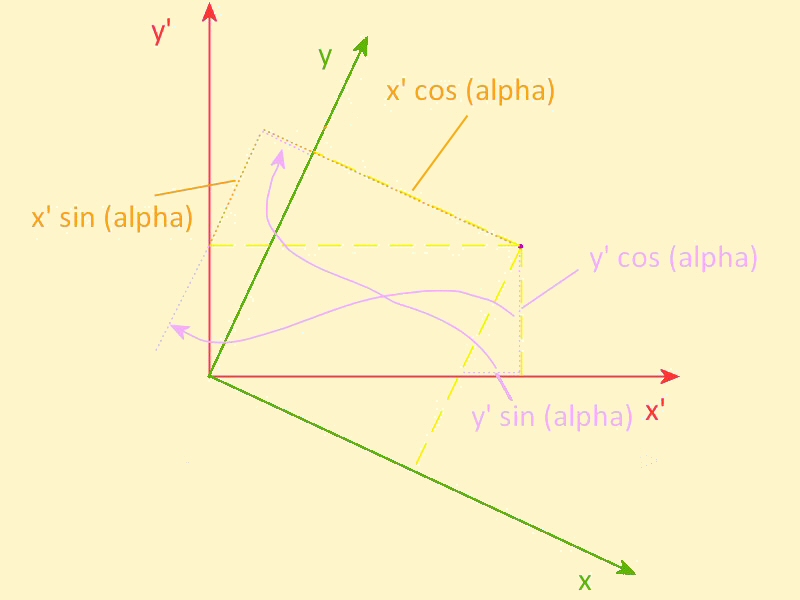
Imagine we have a set of coordinates (4.56201, 2.30556), which we will call x' and y', in a right angle grid, and we would like to transform these to a grid which is identical (same division of, and angle between the axes, same origin), but rotated clockwise around the origin by an angle of alpha, which will here equal 25°, yielding coordinates x and y.
We would have to look up cos 25° and sin 25° in our goniometric tables, and find 0.906308 and 0.422618 respectively.
We can now find the transformed coordinates by solving the following two equations:
x = x' cos (alpha) - y' sin (alpha)
y = x' sin (alpha) + y' cos (alpha)
This yields:
x = 4.56201 x 0.906308 - 2.30556 x 0.422618 = 3.160215
y = 4.56201 x 0.422618 + 2.30556 x 0.906308 = 4.017535
So if we are smart, on a regular four species calculator, we do the following:
Set 4.56201, crank in 0.906308. Reset counter register, set 2.30556, crank in -0.422618. Write down x in the result register : 3.160219
Leave the setting register, clear the counter and result register, crank in 0.906308 again. Reset counter register, set 4.56201, crank in 0.422618. Write down y in the result register : 4.017535
In summary, we have to set three numbers, crank the machine four times, and write down the results. Total time for the calculation done by clumsy me on a Triumphator CN, is 3 min 29 sec.
Now, on a double machine, things become somewhat easier.
On a double Brunsviga D13R1, we set 0.906308 on the left machine, and 0.422618 on the right machine. We set up the machine so both halves rotate in the same direction, then crank in +4.56201.
We reset the counter register and setting registers, but leave the result.
Now we set 0.422618 on the left machine, and 0.906308 on the right machine. We set the machines to rotate in oposite directions (the left machine now turns in the negative direction, taking care of the single negative term), and crank in +2.30556.
We now only have to crank twice, instead of four times. We still have to set 4 input numbers though, which also takes time.
The Odhner 135 follows more or less the same principle, but it is "vorzeichentreu", or "true to sign". The idea of the Odhner factory was that they would make it easy to calculate with complements, which is basically subtracting by adding the complement of the number you want to subtract, and tens' carrying the leading number out of the register. To this end, both setting registers contain an extra pin, which operates 5 pinwheels at the same time, to add all leading nines to the result and effect this carry. To do our calculation, we set 0.906308 on the left machine, and 0.422618 on the right machine, then crank in +4.56201.
We reset the counter and setting registers (the latter simply by hand), but leave the result.
Now we set 0.422618 on the left machine, using the red numbers, so basically from the bottom up. The rightmost column is special, because there the numbers are shifted down by one unit, to effect the carry. The "special pin" on the left of the left machine is set all the way down to red "0" - the left machine now "virtually" turns in the negative direction, taking care of the single negative term. We set 0.906308 on the right machine, and crank in +2.30556.
Total time for either machine: about 2 minutes
In a machine where the result registers can be switched, such as the Thales GEO, the calculation would look like this:
Set 0.906308 in the left machine, and 0.422618 in the right one. Set machines to rotate in the same sense. Crank in 4.56201.
Reset counter register, move carriage all the way to the left, so the right register is under the left machine. Crank in 2.30556.
Move the carriage all the way to the other side, so the left register is onder the right machine. Since this is the negative term, you can simply crank the counter register clear in the negative sense, without having to refer further to any notes.
We now only have two inputs to set instead of four, but have to crank the machine three times, one of which can be very quick, cranking the register clear. Depending on what the numbers are, this can be more economical than in the Brunsviga double machine.
Total time: still about 2 minutes, but I have been unable to make a final run of the calculation because the machine broke down ... see the story about the "naughty Thales GEO".
For the Brunsviga B183 triple machine, things get even easier:
You set 0.906308 in the middle machine, and then use both hands for setting 0.422618 in the both outside machines - this can be done simultaneously.
Now set the carriage under the rightmost two machines, set the machines all in the same direction, set the counter register to counting in the right register only, and crank in 4.56201.
Now set the carriage all the way to the left, set the machines to rotate in opposite directions, so the middle one turns negative, switch the counter register to count on the left side only, and crank in -2.30556 (minus because the results are switched around so the result with the positive term is under the middle machine, which turns in the opposite sense)
With this machine, you have to set 3 numbers (2 simultaneously), and crank twice. At the end of the calculation, the counter registers contain both multipliers for a quick final check to avoid mistakes.
The time with this machine is well under two minutes, and excercising my ability to set two numbers simultaneously would improve on this.
One more I would like to show, that is only sort of a double machine, the Archimedes GEMRZ, which has two independent result registers, but only one input register. However, because it is automatic and electric, it can still save you some time ...
You can set one of the coordinates in the input, and multiply by cos(alpha) in one result register, and by sin(alpha) in the second one. Then you clear the input, set the other coordinate, multiply by cos(alpha) into the second result register, and multiply by sin(alpha) negatively in the first result register. Each result register will now contain a new value for the rotated coordinates.
You have to key in six numbers and wait for the result of 4 runs of the machine, which take about 7 to 10 seconds, so it's down to how fast and correct you can key in the numbers. Slightly over 2 minutes should be feasible.
Here's a video of the process:
Obviously, it pays to keep good track of the signs of the terms, or this will all lead to tears. It also helps to use abridged multiplication if the tens carry in the counter register works properly (i.e. multiply by 10, then substract 1 in order to multiply by 9 - in this case this will save you 7 turns of the crank. It becomes second nature every time you see the numbers 6, 7, 8 or 9 appear). It is also a huge time-saver, when the number of significant digits is different between the various factors in the calculation, to crank the number with the smallest number of digits, and put the longer ones in the setting register. Imagine that the coordinates you need to transform are the pair (3,4). Obviously you would prefer to crank these numbers, and not the six-digit sines and cosines.
For truly general coordinate transformations, there are two more operations, namely bringing the origins of the grids to the same place, which means you must know at least the coordinates of one point in both coordinate systems (preferably the origin of the other one in the grid you're transforming from, but any point can work, it's just more complicated), and this is where it pays to set the coordinates into the setting register and crank the sines and cosines, and not vice versa, as the addition or substraction for the origin shift can then be done prior to the rotation of the grid.
If the machine has backtransfer (and the Brunsvigas do, the Thales GEO doesn't), you set the coordinates, add or subtract the origin shift in both machines at once, and back transfer both results to the setting registers.
You have to write down these origin shifted coordinates, since for a double machine you will have to switch them from the left to the right machine and vice versa in the rotation step as detailed above.
In the B183 this is not necessary, as there you can shift the carriage around, again saving precious time. You will have to set the number that appears in the setting register for the rightmost machine into the leftmost machine, and this still has to be done manually.
Finally, the last step after origin shift and rotation, is to scale the numbers if the scale of both grids is not the same. For this you need to calculate the x/x' and y/y' ratio from beforehand. For transformations between particular much-used coordinate systems, these factors are always the same, and will obviously be stuck on the wall on a piece of paper, or set firmly in the mind of the operator. You can backtransfer the rotated coordinates into the setting register, and finish by cranking in these factors. If they are identical for the x and y axes, it is one operation, if they are different, you have to uncouple the second machine for cranking in the first factor, write down the result, then hook up the second machine and crank in the second factor.
I hope this gives a taste of what those poor geometers and artillerists of days past were up to on a daily basis ... long live the digital computer and GPS!
